Сопрягаемые детали 3 примера

Цель работы: изучить выполнение сопряжений кривых, выполнить чертеж детали с сопряжениями

1. Деление окружностей на равные части

Деление окружности 4 и 8 равных частей

1) Два взаимных перпендикуляра диаметра окружности делят ее на 4 равные части (точки 1, 3, 5, 7).

2) Далее делят прямой угол на 2 равные части (точки 2, 4, 6, 8) (рисунок 1 а).

Деление окружности на 3, 6, 12 равных частей

1) Для нахождение точек, делящих окружность радиуса R на 3 равные части, достаточно из любой точки окружности, например точки А(1), провести дугу радиусом R.(т.2,3) (рисунок 1 б).

2) Описываем дуги R из точек 1 и 4 (рисунок 1 в).

3) Описываем дуги 4 раза из точек 1, 4, 7, 10 (рисунок 1 г).

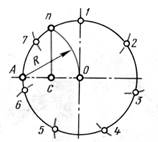
Рисунок 1 – Деление окружностей на равные части

а – на 8 частей; б – на 3 части; в – на 6 частей;

г – на 12 частей; д – на 5 частей; е – на 7 частей.

Деление окружности на 5, 7, равных частей

1) Из точки А радиусом R проводят дугу, которая пересекает окружность в точке n. Из точки n опускают перпендикуляр на горизонтальную осевую линию, получают точку С. Из точки С радиусом R₁=С1, проводят дугу, которая пересекает горизонтальную осевую линию в точке m. Из точки 1 радиусом R₂=1m, проводят дугу, пересекающую окружность в точке 2. Дуга 12=1/5 длины окружности. Точки 3,4,5 находят, откладывая циркулем отрезки, равные m1 (рисунок 1 д).

2) Из точки А проводим вспомогательную дугу радиусом R, которая пересекает окружность в точке n. Из нее опускаем перпендикуляр на горизонтальную осевую линию. Из точки 1 радиусом R=nc, делают по окружности 7 засечек и получают 7 искомых точек (рисунок 1 е).

2. Построение сопряжений

Сопряжением называется плавный переход одной линии в другую.

Для точного и правильного выполнения чертежей необходимо уметь выполнять построения сопряжений, которые основаны на двух положениях:

1. Для сопряжения прямой линии и дуги необходимо, чтобы центр окружности, которой принадлежит дуга, лежал на перпендикуляре к прямой, восстановленном из точки сопряжения (рисунок 2 а).

2. Для сопряжения двух дуг необходимо, чтобы центры окружностей, которым принадлежат дуги, лежали на прямой, проходящей через точку сопряжения (рисунок 2 б).

Рисунок 2 – Положения о сопряжениях

а – для прямой и дуги; б – для двух дуг.

Сопряжение двух сторон угла дугой окружности и заданного радиуса

Сопряжение двух сторон угла (острого или тупого) дугой заданного радиуса выполняют следующим образом:

Параллельно сторонам угла на расстоянии, равном радиусу дуги R, проводят две вспомогательные прямые линии (рисунок 3 а, б). Точка пересечения этих прямых (точка О) будет центром дуги радиуса R, т.е. центром сопряжения. Из центра О описывают дугу, плавно переходящую в прямые — стороны угла. Дугу заканчивают в точках сопряжения n и n₁, которые являются основаниями перпендикуляров, опущенных из центра О на стороны угла. При построении сопряжения сторон прямого угла центр дуги сопряжения проще находить с помощью циркуля (рисунок 3 в). Из вершины угла А проводят дугу радиусом R, равным радиусу сопряжения. На сторонах угла получают точки сопряжения n и n₁. Из этих точек, как из центров, проводят дуги радиусом R до взаимного пересечения в точке О, являющейся центром сопряжения. Из центра О описывают дугу сопряжения.

в

б

а

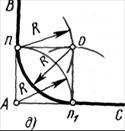
Рисунок 3 – Сопряжения углов

а – острого; б – тупого; в – прямого.

Сопряжение прямой с дугой окружности

Сопряжение прямой с дугой окружности может быть выполнено с помощью дуги с внутренним касанием (рисунок 4 б) и дуги с внешним касанием (рисунок 4 а).

Для построения сопряжения внешним касанием проводят окружность радиуса R и прямую АВ. Параллельно заданной прямой на расстоянии, равном радиусу r (радиус сопрягающей дуги), проводят прямую ab. Из центра О проводят дугу окружности радиусом, равным сумме радиусов R и r, до пересечения ее с прямой ab в точке О1. Точка О1 является центром дуги сопряжения.

Точку сопряжения с находят на пересечении прямой ОО1 с дугой окружности радиуса R. Точка сопряжения С₁ является основанием перпендикуляра, опущенного из центра О1 на данную прямую АВ. С помощью аналогичных построений могут быть найдены точки О2, С₂, С₃.

На рисунке 6 б выполнено сопряжение дуги радиуса R с прямой АВ дугой радиуса r с внутренним касанием. Центр дуги сопряжения О1 находится на пересечении вспомогательной прямой, проведенной параллельно данной прямой на расстоянии r, с дугой вспомогательной окружности, описанной из центра О радиусом, равным разности R-r. Точка сопряжения является основанием перпендикуляра, опущенного из точки О1 на данную прямую. Точку сопряжения с находят на пересечении прямой ОО1 с сопрягаемой дугой.

Рисунок 4 – Сопряжение дуги с прямой

а – с внешним касанием; б – с внутренним касанием.

Сопряжение дуги с дугой

Сопряжение двух дуг окружностей может быть внутренним, внешним и смешанным.

При внутреннем сопряжении центры О и О1 сопрягаемых дуг находятся внутри сопрягающей дуги радиуса R (рисунок 5 а).

При внешнем сопряжении сопрягаемых дуг радиусов R₁ и R₂ находятся вне сопрягающей дуги радиуса R (рисунок 5 б).

При смешанном сопряжении центр О1 одной из сопрягаемых дуг лежит внутри сопрягающей дуги радиуса R, а центр О другой сопрягаемой дуги вне ее (рисунок 5 в).

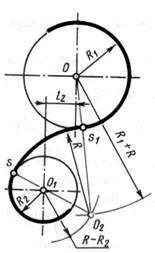
Рисунок 5 – Сопряжения дуг

а – внутреннее; б – внешнее; в – смешанное.

При вычерчивании контуров сложных деталей важно уметь распознавать в плавных переходах те или иные виды сопряжений и уметь их вычерчивать.

Для приобретения навыков в построении сопряжений выполняют упражнения по вычерчиванию контуров сложных деталей. Для этого необходимо определить порядок построения сопряжений и только после этого приступать к их выполнению.

ЗАДАНИЕ: Вычертить изображения контуров деталей, указанных на рисунке задания, нанести размеры. Задание выполнить на листе чертежной бумаги формата А4.

Указания по выполнению задания

При выполнении каждой задачи должна соблюдаться определенная последовательность геометрических построений:

– осевые, центровые линии, основные начертательные;

– обводка, штриховка, выносные линии;

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8752 — | 7489 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

В этой небольшой статье, будут рассмотрены основные виды сопряжений и Вы узнаете о том, как построить сопряжение углов, прямых линий, окружностей и дуг, окружностей с прямой.

Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.

Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.

Ниже будут рассмотрены основные типы сопряжений.

Сопряжение углов (Сопряжение пересекающихся прямых)

Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)

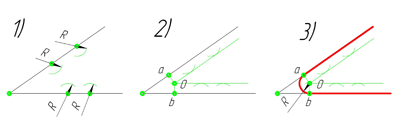
В данном примере будет рассмотрено построение сопряжения прямого угла заданным радиусом сопряжения R. Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом. Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.

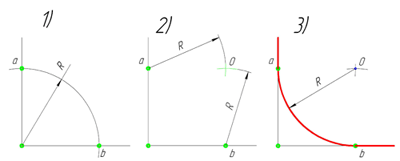
Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)

Ещё один пример сопряжения угла. В этом примере будет построено сопряжение
острого угла. Для построения сопряжения острого угла раствором циркуля,равным радиусу сопряжения R, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b. Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R, соединив точки сопряжения a
и b. Сопряжение острого угла построено.

Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)

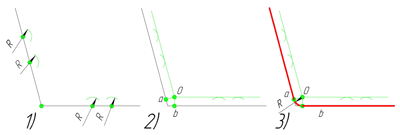
Сопряжение тупого угла строится по аналогии с сопряжением острого угла. Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.

Сопряжение параллельных прямых линий

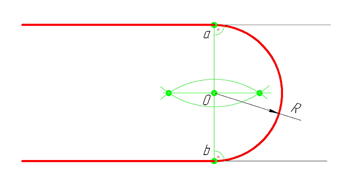
Построим сопряжение двух параллельных прямых. Нам задана точка сопряжения a, лежащая на одной прямой. Из точки a проведём перпендикуляр до пересечения его с другой прямой в точке b. Точки a и b являются точками сопряжения прямых линий. Проведя из каждой точки дугу, радиусом больш отрезка ab, найдём центр сопряжения — точку О. Из центра сопряжения проведём дугу заданного радиуса сопряжения R.

Сопряжение окружностей(дуг) с прямой линией

Внешнее сопряжение дуги и прямой линии

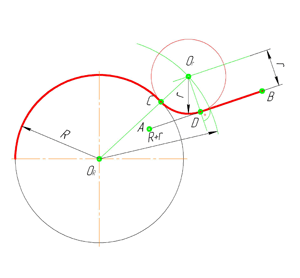
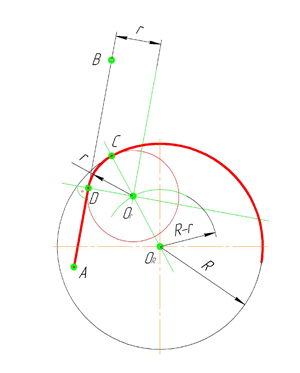
В этом примере будет построено сопряжение заданным радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиусом R.

Сначала найдём центр сопряжения. Для этого проведём прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса сопряжения r, и дугу, из центра окружности O R радиусом R+r. Точка пересечения дуги и прямой и будет центром сопряжения – точкой О r .

Из центра сопряжения, точки О r , опустим перпендикуляр на прямую AB. Точка D, полученная на пересечении перпендикуляра и отрезка AB, и будет точкой сопряжения. Найдём вторую точку сопряжения на дуге окружности. Для этого соединим центр окружности О R и центр сопряжения О r линией. Получим вторую точку сопряжения – точку C. Из центра сопряжения проведём дугу сопряжения радиусом r, соединив точки сопряжения.

Внутреннее сопряжение прямой линии с дугой

По аналогии строится внутреннее сопряжение прямой линии с дугой. Рассмотрим пример построения сопряжения радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиуса R. Найдём центр сопряжения. Для этого построим прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса r, и дугу, из центра окружности O R радиусом R-r. Точка О r , полученная на пересечении прямой и дуги, и будет центром сопряжения.

Из центра сопряжения(точка О r ) опустим перпендикуляр на прямую AB. Точка D, полученная на основании перпендикуляра, и будет точкой сопряжения.

Для нахождения второй точки сопряжения на дуге окружности, соединим центр сопряжения Оr и центр окружности О R прямой линией. На пересечении линии с дугой окружности получим вторую точку сопряжения – точку C. Из точки О r , центра сопряжения, проведём дугу радиусом r, соединив точки сопряжения.

Сопряжение окружностей (дуг)

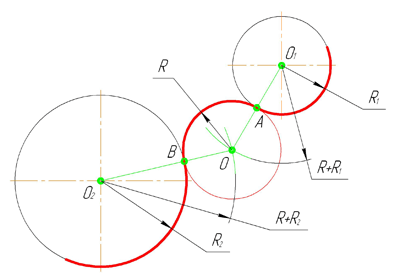
Внешнее сопряжение дуг окружностей

Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей(дуг) O1( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.

Внутреннее сопряжение дуг окружностей

Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На картинке ниже приведён пример построения внутреннего сопряжения окружностей(дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.

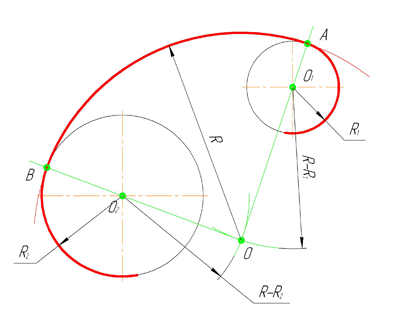
Смешанное сопряжение дуг окружностей

Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На иллюстрации ниже приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.

Сопрягаемые детали— детали, подвижно или неподвижно со­единяемые сборкой и контактирующие друг с другом по сопрягае­мым (после сборки — по сопряженным) поверхностям. Различают охватываемые и охватывающие детали или поверхности, обозначае­мые соответственно . Размеры сопрягаемых поверхно­стей при изготовлении должны находиться в пределах допуска, а при сборке по этим поверхностям могут получаться зазоры S или натяги N за счет деформации соединяемых деталей.

Вал— это наружная охватываемая поверхность.

Отверстие— это внутренняя охватывающая поверхность.

В машиностроении преимущественно применяют посадки системы отверстия. Посадки системы вала применяют для соедине­ния нескольких деталей с гладким валом (штифтом) по разным по­садкам (например, установка нескольких подвижных блоков в обой­ме на одну ось); для установки изделий массового производства в корпусные детали (например, для соединения наружных колец под­шипников качения с корпусами). В приборостроении точные оси малого диаметра (менее 3 мм) часто изготавливают из гладких ка­либрованных прутков, в этих случаях система вала находит широкое применение. При выборе квалитетов необходимо учитывать ряд об­щих положений.

Наличие посадок и их видов. В интервале размеров от 1 до 500 мм посадки с зазором установлены в квалитетах 4-12, переход­ные — в квалитетах 4-7, посадки с натягом — в квалитетах 5-8. Если вид посадки определяют по результатам расчета, то квалитет выби­рают одновременно с посадкой. При подборе квалитетов часто ис­пользуют опыт проектирования и эксплуатации аналогичных изде­лий. В машинах и приборах при высоких требованиях к ограничению разброса зазоров и натягов посадок применяют для отверстий квалитет 7, для валов квалитет 6; при особо высоких требованиях к точности соединений (узлы подшипников качения высокой точно­сти в приборах) применяют для отверстий квалитет 6 и для валов квалитет 5; при менее высоких требованиях к ограничению разброса зазоров и натягов для упрощения технологии можно применять ква­литет 8; в соединениях, допускающих большие зазоры, и для облегчения сборки применяют квалитеты 9-12; допуски свободных разме­ров назначаются по квалитету 12 и грубее. Учитывая повышенные требования к качеству машин и приборов, рекомендуется шире при­менять квалитеты 6-8.

Основной причиной потери работоспособности машинами се­рийного выпуска является снижение точности в результате износа основных деталей и соединений, поэтому в настоящее время распро­странен метод назначения допусков и выбора посадок с зазором, ос­нованный на гарантированных запасах точности эксплуатационных показателей машин. Суть этого метода заключается в том, что на ос­новные детали и соединения назначают несколько завышенные до­пуски, которые должны обеспечивать эксплуатационные показатели машин (точность вращения шпинделя, перемещения суппорта и пр.), а также компенсировать погрешности изготовления и сборки. Такой допуск называют функциональным. Он включает в себя эксплуатаци­онный допуск, обеспечивающий запас точности деталей и их соеди­нений с целью сохранения работоспособности машины в течение на­меченного срока службы, и конструктивный допуск, обеспечивающий компенсацию погрешностей изготовления деталей и сборки изделий. Таким образом, функциональные допуски отдельной детали и посад­ки с зазором будут определяться суммой названных допусков.

Выбор посадок. Основными характеристиками посадок явля­ются наименьшие натяги или зазоры и их допуски. При переходе от посадок с большими зазорами (образованными полями а, А) к по­садкам с большими натягами (образованными полями zc, ZC) при неизменном номинальном размере наименьшие зазоры уменьшают­ся и наименьшие натяги увеличиваются. У переходных посадок в том же направлении (от поля j_s, J_s к полю и, N) повышается веро­ятность получения натягов. При переходе к менее точным квалитетам при одинаковых посадках и номинальных размерах значения S_min и N_min не изменяются, но допуски посадок при этом увеличива­ются. Например, допуск посадки аза больше допуска посадки С увеличением допуска посадки утрачивают определенность характера соединения, что особенно нежелательно для посадок с натягами и переходных. Поэтому указан­ные посадки образуют полями допусков не грубее Для правиль­ного применения посадок необходимо знать их основные свойства.

Посадки с натягомпо значению гарантированного натяга подразделяют на три подгруппы. Посадки с минимальным гаранти­рованным натягом применяют при малых нагрузках и для уменьшения деформаций собранных деталей. Неподвижность соединения обеспечивают дополнительным крепле­нием. Эти посадки допускают редкие разборки. Посадки с умерен­ными гарантированными натягами

допускают передачу на­грузок средней величины без дополнительного крепления, а также с дополнительным креплением; могут применяться для передачи больших нагрузок, если прочность деталей не позволяет применить посадки с большими натягами, сборка может производиться под прессом или способом термических деформаций. Посадки с боль­шими гарантированными натягами

передают тяжелые и динамические нагрузки без дополнительного крепления. Необходима проверка соединяемых деталей на прочность; сборка осуществляется в основном способом термических деформаций.

Переходные посадкиобразуются полями допусков, которые установлены в квалитетах 4-8 и характеризуются возможностью по­лучения сравнительно небольших зазоров или натягов. Они приме­няются в неподвижных разъемных соединениях при необходимости точного центрирования, при этом необходимо дополнительное кре­пление собранных деталей. Посадки с более вероятными натягами

применяют при больших удар­ных нагрузках, при повышенной точности центрирования и редких разборках, а также при затрудненной сборке вместо посадок с ми­нимальным гарантированным натягом.

Посадки с равновероятными натягами и зазорами

имеют наибольшее применение из переходных посадок, так как для сборки и разборки не требуют больших усилий и обес­печивают высокую точность центрирования. Посадки с более веро­ятными зазорами применяют при небольших статических нагрузках, частых разборках и затрудненной сборке, а также для регулирования взаимного положения деталей.

Посадки с зазоромобразуются полями допусков установлены в квалитетах 4-12 и применяются в неподвижных и подвижных соединениях для облегчения сборки при невысокой точности центрирования, для регулирования взаимного положения деталей, для обеспечения смазки трущихся поверхностей (подшип­ники скольжения) и компенсации тепловых деформаций, для сборки деталей с антикоррозийными покрытиями. Посадки с обеспечивают высокую точность центрирования и поступательного перемещения деталей в регулируемых соединениях и могут заме­нять переходные посадки.

Для подбора посадок применяют методы подобия и расчет­ный. В методе подобия используют рекомендации по применению различных посадок, разработанных в результате обобщения опыта проектирования и эксплуатации разнообразных машин, механизмов, приборов. При подборе посадок необходимо учитывать конструк­тивные и эксплуатационные особенности проектируемого соедине­ния. Например, зазоры и натяги для стандартных посадок установ­лены для следующих условий: нормальная температура работы со­единение соединяемые детали изготовлены из материалов с одинаковыми или близкими температурными коэффициентами линейного расширения; отношение длины соединения к диаметру Если перечисленные условия не выполнены, то выбор по­садок корректируется. При принимают посадки с больши­ми зазорами, а при — с меньшими.

При больших тепловых деформациях отверстия выбирают по­садку с уменьшенным зазором, а при больших тепловых деформа­циях вала — с увеличенным зазором. Для посадок с натягами при ма­лой длине напрессовки увеличивают натяги и уменьшают их с уве­личением длины; для соединения тонкостенных деталей или дета лей, изготовленных из малопрочных материалов, применяют посад­ки с меньшими натягами и т.д. Метод подобия характеризуется от­сутствием точных критериев и требует большого опыта проектиро­вания. Расчетный метод дает более обоснованные результаты. Одна­ко неисчерпаемое разнообразие соединений препятствует созданию универсального метода расчета посадок.